Visual Basic program "VB Hubble" - Description and operation

Contents

• Description
• Operation - Control Form
• Description Display Form
• Description Print Form
• Program Evalution
• Reflection
• FeedBack

Introduction and Purpose

The purpose of the Visual Basic program "VB Hubble" is:

1. To demonstrate Hubble's Law. This is done by means of a binary star system of two "large" stars and a third smaller star
2. To demonstrate the behaviour how a third star can influence the behaviour of a binary star system.
   In a wider perspectif this can also be seen of how stable a binary star system is.
   To download an executable select: VB Hubble.zip
   This zip file contains 1 program: VB Hubble.exe" is written in Visual Basic 5.0. For more information goto: Implementation details
   
   • The same program is also available in Quick Basic as "Hubble.bas".
     
     For a description select: Program "Hubble". Hubble's Law with 3 stars
     For a copy of hubble.exe select: hubble.zip.
     

Description

The Visual basic program program "VB Hubble" consits of 3 Forms (or displays):

• Control Form. This form is used to Start the program and to modify the parameters.
• Display Form. This form shows the results of the simulation in a graphical form.
• Print Form. This form shows the results of the simulation in a text form.

Operation - Control Form

Operation of the program is done from the Control Form.

Picture 1A

Picture 1B

Picture 1A Shows the initial display.
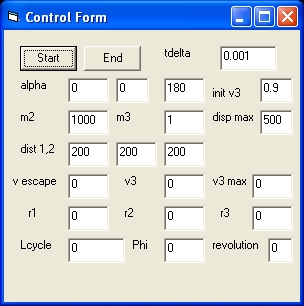
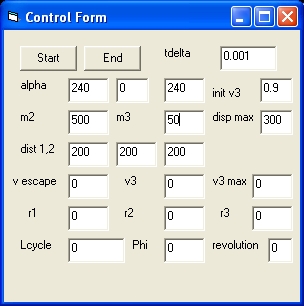
This dispay shows 3 Commands: Start, End and Stop. This depends about were you are during program execution.

• The Start command is used to start the program
• The End command is used to terminate the program
• The Stop command is used to stop the simulation

After startup the Control Form shows 6 Parameters which can be selected: tdelta, alpha left, alpha right m #3, init v #3 , disp max ,

• tdelta shows the step size. The standard value is 0.005
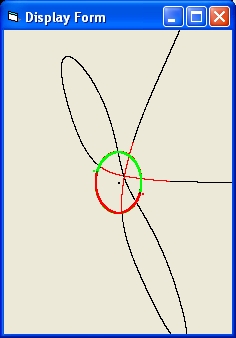
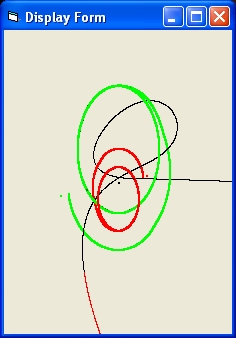
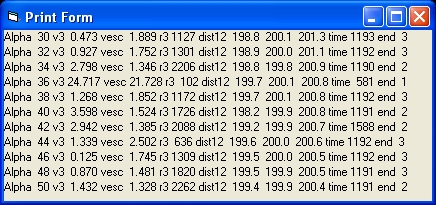
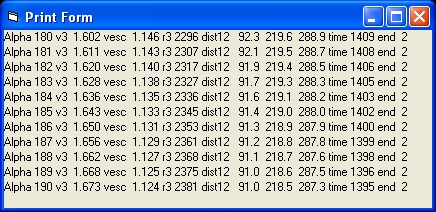
• The parameter alpha shows three values: the initial value, the average value and the final value in degrees of the angle between m1 and m2.
  Only the initial value at the left and the final value at the right can be modified.
• m2 is the mass of m2. The mass of m1 = 1000.
• m3 is the mass of m3. The standard value = 1
• init v3 initial fraction of the speed v3 versus the escape velocity. Standard value is 0.9
• disp max display size divided by 2.
  Because the initial distance of m2 is 500 in the x direction the standard vale is also 500.

The Control display also shows the following additional parameters:

• v escape is the actual escape velocity of m3
• v3 is the actual velocity of m3
• r3 is the actual distance of r3 from the center of the binary stars
• Lcycle is the actual number of iterations or program cycles in the simulation
• Phi is the actual angle between m1 and m2
• revolutions is the actual number of revolutions of

Display Form

The "Display Form" shows the result of the simulation.
In the center of the display the two large objects are rotating, counter clockwise, around each other.
With the parameter alpha is equal to zero, m1 starts from the left in red at 9 o'clock and m2 from the right in green at 3 o'clock. m3 always comes from the right in black.

Picture 2A

Picture 2A shows one result of the standard simulation with the parameters of Picture 1A. The parameter m1 = 1000, m2 = 1000 and m3 = 1. The parameter alpha is 160 degrees. The black dot in the center is the center of gravity of the binary pair. With the parameter alpha is equal to 160, m1 starts at roughly 4 o'clock in red and m2 in green at 10 o'clock. Object m3 comes in from the left below the escape velocity in black. When m3 approaches the center of the binary pair its speed increases above the escape velocity. This is indicated by the red color. At that moment m1 in red is at roughly 12 o'clock. Because m3 is closer to m1 than towards m2 its path will be bended towards roughly 11 o'clock The speed of m3 decreases, goes below the escape velocity and the color changes back to black. Because the speed goes below the escape velocity it will again be atracted towards the binary pair. The whole process repeats itself but now roughly at 5 o'clock. And again but now roughly at 1 o'clock. The simulation stops because of distance limitation and after 3 revolutions of the binary pair. Picture 1A shows the initial and final results of the control form

Picture 2B

Picture 2B shows one result of the standard simulation with the parameters of Picture 1B. The parameter m1 = 1000, m2 = 500 and m3 = 50. The parameter alpha is 240 degrees. With the parameter alpha is equal to 240, m1 in red starts at roughly 1 o'clock and m2 in green at roughly 7 o'clock green. Object m3 comes in from the left in black. Is reflected first by m2 in green and moves towards 6 o'clock and than moves back towards the center towards m1 in red. This whole interplay between the three objects continues for at least 10 revolutions and maybe forever. The interesting part of this simulation is that the speed of m3 always stays below the escape velocity. Picture 1B shows the initial and final results of the control form

Picture 2C

Picture 2C shows: The parameter alpha is 190 degrees. The parameter m1 = 1000, m2 = 500 and m3 = 50 . With the parameter alpha is equal to 190, m1 in red starts at roughly 1 o'clock and m2 in green at roughly 7 o'clock. Object m3 comes in from the left in black. Is first atracked towards m1 in red. The path makes always a complete circle around m1 and is then atracked towards m2 in green. Its speed increases above the escape velocity and m3 (now in read) leaves the binary pair. What is interesting about this simulation is that its brings the two binary stars in close approximation.

In order to test the stability issue the masses of the three objects are respectivily 1000, 500 and 50.
The following table shows the results:

3 Objects m0, m1 and m2 Demonstration Delta time 0,001 init v3 0,9 # stars 3 alpha 0 m1 1000 m2 500 m3 50 Alpha 0 v3 0.912 vesc 1.266 r3 1881 dist12 166.7 197.3 229.0 time 1318 end 3 Alpha 20 v3 1.503 vesc 1.127 r3 2353 dist12 163.4 190.6 217.7 time 1254 end 2 Alpha 40 v3 2.176 vesc 1.028 r3 2819 dist12 152.6 182.0 208.5 time 1165 end 2 Alpha 60 v3 24.296 vesc 20.827 r3 103 dist12 199.5 199.8 201.9 time 133 end 1 Alpha 80 v3 1.797 vesc 1.068 r3 2602 dist12 160.8 188.0 214.0 time 1231 end 2 Alpha 100 v3 0.850 vesc 1.250 r3 1892 dist12 173.2 197.9 223.3 time 1336 end 3 Alpha 120 v3 3.712 vesc 2.773 r3 371 dist12 182.2 209.3 239.3 time 1465 end 3 Alpha 140 v3 0.197 vesc 1.499 r3 1304 dist12 146.9 213.1 263.6 time 1917 end 3 Alpha 160 v3 1.458 vesc 1.211 r3 2082 dist12 98.5 220.8 290.7 time 1430 end 2 Alpha 180 v3 1.602 vesc 1.146 r3 2296 dist12 92.3 219.6 288.9 time 1409 end 2 Alpha 200 v3 1.680 vesc 1.120 r3 2387 dist12 92.6 217.4 285.1 time 1387 end 2 Alpha 220 v3 15.854 vesc 14.850 r3 112 dist12 190.9 201.0 228.3 time 256 end 1 Alpha 240 v3 2.158 vesc 4.218 r3 255 dist12 163.4 243.7 314.0 time 6284 end 4 Alpha 260 v3 17.229 vesc 16.025 r3 104 dist12 199.8 200.0 202.9 time 119 end 1 Alpha 280 v3 2.980 vesc 0.985 r3 3116 dist12 121.4 174.8 217.1 time 1052 end 2 Alpha 300 v3 2.268 vesc 1.045 r3 2765 dist12 141.3 183.8 221.5 time 1163 end 2 Alpha 320 v3 1.661 vesc 1.126 r3 2386 dist12 153.6 190.7 226.3 time 1243 end 2 Alpha 340 v3 1.085 vesc 1.235 r3 1985 dist12 162.2 196.3 230.7 time 1304 end 3 Alpha 360 v3 0.912 vesc 1.266 r3 1881 dist12 166.7 197.3 229.0 time 1318 end 3 NEXT TEST ? Table 2

In all the simulations the average distance between m1 and m2 is roughly 200.
The simulations between alpha is 160 and alpha = 200 are the most remarkable. In these cases the minimum distance is roughly 100 and the maximum distance is 300. That means the path of a stable binary star system changes from a circle into an ellipse.
For more detail see Picture 2C

The case with alpha 240 is interesting because m3 is captured and the binary system changes into a threesome. This is a stable configuration. For more detail see Picture 2B

---

Reflection

What the standard configuration indicates that it is rather simple to have configurations that ejected stars do not follow Hubble's law i.e. that the speed of the ejected star is not a simple function of distance.

---

Feedback

None

---

Created 22 Februari 2016

Back to my home page: Contents of This Document